Stream Fusion is PEF-ible

Over the year, we have mostly looked at partial evaluation for performing shortcut fusion. I was studying whether, and how easily, these algorithms can be expressed in a partial evaluation framework.

The adventure led me to implement shortcut fusion, with satisfactory results (here, here, here mostly, but also here and here).

After quite a bit of time, I’m happy to say that Stream Fusion [1] is also PEF-ible (Partial Evaluation Fus-ible). In this post, we’ll go into details of how, and also see some potential caveats/limitations. Though we have seen the stream library before, we will rebuild it from first principles, and then fuse it. It turns out that a lot of the difficulties come with trying to fuse flatMap. In the end, I have been, unsurprisingly, inspired by related Haskell work [3, 5].

Quick Recap

Just to recap, the idea of fusion is to remove intermediate datastructures created in a pipeline of operations. We would also like our fusion algorithm to have the following desirable properties:

  1. The algorithm should work for as many different list operations as possible.
  2. The algorithm should be simple, elegant even.

The first fusion algorithm we studied, foldr/build, is simple and elegant. Yet we can’t fuse the zip function easily with it. This is because zip is not well expressed as a fold operation: fold is an inherently push-like operation, whereas zipping two lists requires us to pull elements from 2 lists before packaging and pushing a pair further downstream.

List Operations as Unfolds

We looked at list operations in terms of fold operations previously. But we can also look at them in terms of unfolds. For this, we will use a classical category theory trick, flipping the arrows. Recall that fold is a function that, given an algebra F[S] => S, yields a function from Fix[F] => S. We are interested here in the list algebra:

L_alg[T] = forall S. (() + A x S) => S

where the list functor, for elements of type A, is forall S. () + A x S (and empty list, or an element followed by a list). Therefore, the fold function on the list algebra can be written as:

fold: forall S. List[A] => ((() + A x S) => S) => S

Exercise 1: Flip the arrows in the above definition. What do you get?

Parenthesis: Flipping the arrows in category theory usually gives us the dual concept. While fold uses the fact that there is a unique morphism from an initial algebra to any other algebra, unfold uses the fact that there is a unique morphism from a final co-algebra to any other algebra. It turns out that for lists, both co-incide. Hinze et al. call these recursive co-algebras. Please do take a look at their paper for more details, and a better explanation [2].

For the above, we get:

unfold: forall S. S => (S => (() + A x S)) => List[A]

How do we read this function? Well:

Exercise 2: What concept does the above remind you of?

The inner function, given a state, either says it is done, or gives a new element. In other words, it either has a next element, in which case you can get it, or it is done. Indeed, we have, here an implementation of functional iterators. Before creating a library of iterators, let’s exercise some intuition over unfold first:

Exercise 3: Implement the body of unfold, if possible in a tail-recursive way. If the source itself is a List[A], what function do you pass to unfold? What about a range iterator? Can you also implement map for lists?

def unfold[S, A](step: S => Option[(A, S)])(seed: S): List[A] = ???
def unfoldList[A](ls: List[A]): List[A] = unfold[???, ???](???)(???)
def unfoldRange(a: Int, b: Int): List[Int] = unfold[???, ???](???)(???)
def map[A, B](ls: List[A], f: A => B): List[B] = unfold[???, ???](???)(???)

The not-so-usual suspects

Now that was easy. What about our good friends filter and flatMap?

Exercise 4: Implement filter on lists using unfold:

def filter[A](ls: List[A], p: A => Boolean): List[A] = unfold[List[A], A](???)(ls)

That looks trickier. The problem is with the step function. What if an element of the ls does not satisfy the predicate? What do we generate then? The most direct approach seems to create a function that calls itself recursively:

def filter[A](ls: List[A], p: A => Boolean): List[A] = {

  def inner(tmpSource: List[A]): Option[(A, List[A])] = tmpSource match {
    case Nil => None
    case x :: xs =>
      if (p(x)) Some(x, xs)
      else inner(xs)
  }

  unfold[List[A], A](inner _)(ls)
}

In this implementation, the work of unfolding a source is shared by the unfold as well as the inner, recursive function. In fact, inner is doing the lion’s share, since it is responsible for discarding all elements that don’t pass the predicate.

We may desire to have a non-recursive implementation, since unfold is already a recursive scheme. Here’s a way to achieve that:

 def filter[A](ls: List[A], p: A => Boolean): List[A] = {

  val intermediate: List[Option[A]] = unfold[List[A], Option[A]]{
    case Nil => None
    case x :: xs =>
      if (p(x)) Some((Some(x), xs))
      else      Some(None, xs)
  }(ls)

  intermediate.foldRight(List[A]()){
    case (Some(a), acc) => a :: acc
    case (_, acc)       => acc
  }

}

We bump satisfying elements by wrapping them in an Option, and then collapse the list using foldRight. The advantage is that we keep our filter operation in a single pipeline, but it seems that we create an extra, intermediate list. To some extent, we are also cheating a bit by using a fold following the unfold.

Exercise 5: Implement flatMap on lists using unfold:

def flatMap[A, B](ls: List[A], f: A => List[B]): List[B] = ???

This one is even more tricky. While unfolding the outer list ls, when we encounter an element a: A, we get a new list of type B by applying f. And we must pull out these elements one by one. We must somehow store some information as to whether we are processing an internal list, or an outer one. Here is a way to do that:

def flatMap[A, B](ls: List[A], f: A => List[B]): List[B] = {

  val innerList: List[Option[B]] = unfold[(List[B], List[A]), Option[B]] {
    case (Nil, Nil) => None
    case (Nil, a :: as) => Some((None, (f(a), as)))
    case (b :: bs, as) => Some((Some(b), (bs, as)))
  }((Nil, ls))

  innerList.foldRight(List[B]()){ case (elem, acc) => elem match {
    case None => acc
    case Some(b) => b :: acc
  }}
}

The intuition is similar to the second implementation of filter: when in doubt, introduce an extra box. We are not unfolding over ls only, but a pair containing the outer and possible inner lists. When both inner and outer lists are empty, we are done. As long as there is an element in the inner list, we return it, as an Option[B]. If the inner list is empty, we create a bubble (None), while getting the new inner list. Once again, as the list has bubbles, we need to remove them (here using foldRight). Before moving on, a final, simpler, exercise:

Exercise 6: Implement zip on lists using unfold:

def zip[A, B](as: List[A], bs: List[B]): List[(A, B)] = ???

Iterators, or Streams, as a Staged Library

Previously, we built a library out of folds, because we could express many list operations as fold, and fusing a pipeline of folds was easy. Now we attempt the same with unfold. We have gained one extra operation, zip, at the cost of making the implementations of filter and flatMap more complex. Stay tuned, we will discuss later why we even need to bother.

As seen above, unfolds are a more theoretical name for functional iterators, or, as the Haskell folks know it, streams. We’ll also call our Scala library Streams, because after all, Scala is a gateway drug to Haskell.

Since we are already familiar with staging, we will also use the Rep hammer whenever it seems right. Here is a first design proposal:

trait Streams
    extends FoldLefts
    with ... {

  abstract class Stream[A: Typ] { self =>

    type Source
    implicit def sourceTyp: Typ[Source]

    /** The initial source provided to the iterator */
    def source: Rep[Source]

    def atEnd(s: Rep[Source]): Rep[Boolean]
    def next(s: Rep[Source]): Rep[(A, Source)]

    def toFold: FoldLeft[A] = new FoldLeft[A] {
      def apply[Sink: Typ](z: Rep[Sink], comb: Comb[A, Sink]): Rep[Sink] = {

        var tmpSource = source
        var tmpSink = z

        while (!atEnd(tmpSource)) {
          val elem: Rep[(A, Source)] = next(tmpSource)
          tmpSink = comb(tmpSink, elem._1)
          tmpSource = elem._2
        }

        tmpSink
      }
    }
  }
}

Essentially, a stream pulls elements of type A from a source. The type of this source (capital Source) is given as a type member, instead of a type parameter. This gives us flexibility in choosing the type of the source when we need to. Also, this means that we do not know (need to know) the type of a source when dealing with an iterator.

Exercise 7: You will notice that we are mixing in FoldLefts, and that a stream has a toFold method. Why?

This is a rather nice feature. In the previous section, we looked at unfolding into lists exclusively. Nothing prevents us from unfolding into some other structure, for example an integer (for sums). And we already have a way of doing that, through folds! The toFold function simply says: from this point on, I will be working with folds. I will eventually tell you (the pipeline) what to fold into (the Sink type), but for now, I do not know yet.

Of Bananas, Lenses, and Envelopes

This may sound a little bit confusing. When implementing the staged fold library, we did not need to connect an unfold to a fold, but we are when it is the other way around. Why?

In fact, we did connect an unfold even back then. We did it very subtly. Indeed, a fold created from a list or a range, pulls elements out of these, until the list or range has been covered. For example, if we look at the definition of foldLeft on lists:

def foldRight[A, B](z: B)(comb: (A, B) => B)(ls: List[A]): B = ls match {
  case Nil => z
  case x :: xs => comb(x, foldRight(z)(comb)(xs))
}

We are unfolding the input list ls with the pattern match x :: xs. This is equivalent to calling the step function.

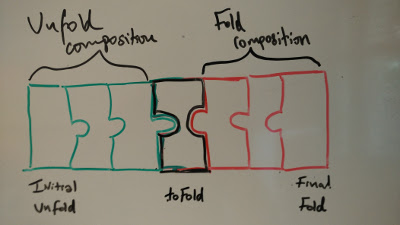
The fold-unfold puzzle

The main difference between both libraries is our decision to compose over folds rather than unfolds (or vice versa). But in both cases, the pipeline has to be closed, on one side or the other. You may have stumbled on literature which talks about such things, using more complicated words. Let’s take a minute to fill the vocabulary gaps:

Exercise 8: Great, we can plug a fold to an unfold to a fold. Implementing filter and flatMap for folds is easier. So why all the fuss?

Indeed, it seems that we can handle quite a few interesting cases, even with zip. Given the pipeline:

(xs zip ys) map (f1) flatMap (f2) filter(p1)

we can transform it to:

Stream.from(xs).zip(Stream.from(ys)).toFold.map(f1).flatMap(f2).filter(p1)

and get the whole pipeline fused! If we have a filter preceding a zip, this wouldn’t be possible. Once we have crossed over to the fold world, there is no coming back. Hence we still need to have implementations of filter and flatMap in the unfold world:

(xs filter p1) flatMap (f1) zip ys

Filter on Streams

Let us now move on, and implement filter on streams.

Exercise 9: From the two filter implementations that use unfold above, which one should we pick?

Based on previous lessons learnt, we will want to avoid a recursive implementation. From a staging point of view, a recursive implementation means that we have to generate a recursive function (Rep[A => B] as opposed to Rep[A] => Rep[B]). If we want to fuse functions following a filter in the pipeline, it would make it harder.

You may wonder why an implementation of filter as in the standard library for Iterator does not work. This implementation does not introduce an extra box, nor is it recursive. Instead, it uses mutable variables to maintain the current state of a stream. Ultimately, it is an implementation of the recursive solution, but using mutable variables and loops. But, as DarkDimius pointed out, we call next at two different places, and therefore risk exploding code generation (links for code below). Also, Amir tells us that it generates slow code.

It is better to create a box, and preserve a single pipeline. As we saw before, we can quite easily get rid of these boxes using CPS encodings.

Exercise 10: Should filter on streams therefore return a Stream[OptionCPS[A]]?

There is a hidden question here. The above implementation of filter creates an intermediate List[Option[A]] and immediately proceeds to remove all bubbles using a fold. But we may want to delay this folding, as discussed, and hence propagate the bubbles until the very end.

Returning a Stream[OptionCPS[A]] breaks composition however. Any function following such an implementation will have to work on an OptionCPS[A], instead of a simple A. Worse, a filter followed by a filter creates nested boxes. We must imperatively maintain the original signature. An elegant solution is to bake the bubble system into the implementation of Stream directly. This means that the next function will always return an OptionCPS[A]. This is internal to the implementation of streams, and does not show up in the interface:

trait Streams
    extends FoldLefts
    with OptionCPS {

  abstract class Stream[A: Typ] { self =>

    type Source
    implicit def sourceTyp: Typ[Source]

    /** The initial source provided to the iterator */
    def source: Rep[Source]

    def atEnd(s: Rep[Source]): Rep[Boolean]
    /** baking in the `Option` here */
    def next(s: Rep[Source]): Rep[(OptionCPS[A], Source)]

    def toFold: FoldLeft[A] = new FoldLeft[A] {
      def apply[Sink: Typ](z: Rep[Sink], comb: Comb[A, Sink]): Rep[Sink] = {
        var tmpSource = source
        var tmpSink = z

        while (!atEnd(tmpSource)) {
          val elem: Rep[(OptionCPS[A], Source)] = next(tmpSource)
          /**
           * The key step. This is where we peel out the option
           */
          elem._1.apply(
            _ => (),
            x => tmpSink = comb(tmpSink, x)
          )
          tmpSource = elem._2
        }
        tmpSink
      }
    }
  }
}

Note that this affects the implementation of toFold. We just peel out the box at the very end, and it remains a fairly simple change.

Paying dues

This idea of introducing an extra box did not appear to me, unfortunately. In fact, this is the key, and in my opinion, beautiful insight of the Stream Fusion paper. They present it in the form of the Step data type, but it is essentially the same thing.

Exercise 11: Implement map, filter and zip on Stream:

def map[B: Typ](f: Rep[A] => Rep[B]): Stream[B] = ???
def filter(p: Rep[A] => Rep[Boolean]): Stream[A] = ???
def zip[B](that: Stream[B]): Stream[(A, B)] = ???

FlatMap, the big one

We can finally attack the tough guy, flatMap. Let us look at the definition we wish for the the function:

def flatMap[B: Typ](f: Rep[A] => Stream[B]): Stream[B]

If f produces a static stream based on a given value of type Rep[A], it is ideal. This is analogous to the flatMap implementation on folds. And there are quite a few cases where this applies. For instance, nested integer ranges fall under this category:

for (i <- 1 to 10; j <- 1 to i) yield j

The range 1 to i is statically known once we know i. Therefore, a nested stream over such a range is also statically known. The signature of flatMap on Stream is, however, much more powerful. Remember that every Stream has an internal Source type. A function passed to flatMap can, for a given value of type Rep[A], produce a stream with any possible Source type. Thus all bets are off, and we would be forced to work with a signature where the stream is indeed dynamic (note the additional Rep):

def flatMap[B: Typ](f: Rep[A] => Rep[Stream[B]]): Stream[B]

Another way to look at the issues

Let us take a step back, and reason about streams without Rep.

Exercise 12: What is the inner Source type of a Stream resulting from a flatMap:

//no Reps
def flatMap[B](f: A => Stream[B]): Stream[B] = new Stream[B] {
  type Source = ???
}

Recall, from the earlier implementation using unfold, that the source contained information of the outer, as well as the inner list. As we do not know the type of the inner source, the source type has to be

type Source = (self.Source, Option[Stream[B]])

The implementation of next follows its list counterpart. If there is an inner stream available, we get an element from it. If not, we propagate a bubble, and at the same time get a new inner stream from an element of the outer stream.

In the general case, deforesting the nested stream is not possible, precisely because the inner source type differss every time a new stream is computed. With the general signature, we would have to

The original Stream Fusion work does the above, with the help of transformations such as static-argument transformation.

Another approach is possible! If it is easier to implement a version of flatMap where the inner source type is static, why not restrict the signature of flatMap, or of the streams, to reflect this? It does seem that quite a few uses of the function do not need the extra power (to be fair, I haven’t counted these cases, nor know of any literature which does), so we should not be losing too much either. Following this line of thought, the new signature for streams reveals the internal source type as a type parameter:

abstract class Stream[A: Typ, Source: Typ] { self =>
  def source: Rep[Source]
  def atEnd(s: Rep[Source]): Rep[Boolean]
  def next(s: Rep[Source]): Rep[(Option[A], Source)]

  def toFold: FoldLeft[A] = ...

  /** higher-order functions */
  def map[B: Typ](f: Rep[A] => Rep[B]) = new Stream[B, Source] ...
  def filter(p: Rep[A] => Rep[Boolean]) = new Stream[A, Source] ...
  def zip[B: Typ, S2: Typ](that: Stream[B, S2]) = new Stream[(A, B), (Source, S2)] ...

  def flatMap[B: Typ, S2: Typ](f: Rep[A] => Stream[B, S2]):
    Stream[B, (Source, Option[(A, S2)])] = ...

I will not paste the body of flatMap here, as it is analogous to the implementation using unfold on list. Please look at the source code (links below) for the complete thing. Some important points though:

Paying dues, part 2

For a long time I was struggling to express the idea of knowing the source type statically. Then, one fine day, I re-discovered that a similar idea was present all along, first in Coutt’s thesis [5], and then implemented by Farmer et al. in the HERMIT framework [3]. They refer to it as the name-capturing flatten. Moral of the story: read more Haskell papers.

The bottomline

This post closes, for now, a pretty long struggle of mine with fusion. Turns out that stream fusion is, after all, expressible in a partial evaluation framework! It is encouraging to see indeed. While a framework like LMS may be hard for a general programmer, many PE ideas are being progressively integrated into more mainstream languages/systems. Knowing that stream fusion can also be PEF-ed means that it is hopefully on the cusp of being available to the masses.

The code

The code used in this post can be accessed through the following files:

References

  1. Stream Fusion: from lists to streams to nothing at all, Coutts et al. , ICFP 2007
  2. Theory and Practice of Fusion, Hinze et al., IFL 2010
  3. The HERMIT in the Stream, Farmer et al., PEPM 2014
  4. Functional programming with bananas, lenses, envelopes and barbed wire, Meijer et al., FPCA 1991
  5. Stream Fusion: Practical shortcut fusion for coinductive sequence types, Coutts, PhD Thesis 2010
Manohar Jonnalagedda 13 January 2016